The West That Wasnt: Appendix - 1, Action Cards

The action cards contained in The West That Wasnt look very different from cards used in other games. To many, their layout might not seem intuitive. Information is densely packed, yet it is also distributed consistently to make referencing them simple. Introductory instructions on their use can be found in Chapter 3: Action Resolution. This appendix covers the minute details of the layout, as well the how and why of the entries on the cards themselves.

The Four Corners

Every action card has a number in 3 corners, and either yes or no in the other. These entries can be used for various situations, but their meanings describe the origin of the action cards themselves. None of the corner results are randomly distributed. In other words, as will be come clear later, knowing the number in the upper left will also allow the other corner results to be derived, while knowing the upper right and lower left will allow the upper left to be derived.

Upper Left

In the upper left corner is a number from 0 to 53, referred to as number. The action card deck is 54 cards, based on a standard poker deck with jokers included. Each card has a "value" (more on this later), and that is what determines the number in this location. The higher the number, the higher the value. Numbers in this location are unique, so when a card is referenced, this is what is used.

Upper Right

The number in the upper right range from 0-14 and represent the rank of the card, with the jokers being 0 and 14. The rank is in order based on poker rules, with the deuce being 1 (the lowest) and ace being 13 (the highest). There are four each of the 1-13, and one each of 0 and 14 (the jokers). These numbers are called fragments.

Lower Left

The lower left represents the suit of the card, in alphabetical order: clubs (1), diamonds (2), hearts (3), spades (4). The jokers are assigned based on color, with the red joker being zero, and the black being 5. These numbers are called steps. There are 13 of each fragment from 1-4, and one each of 0 and 5 (again, the jokers).

Lower right

The lower right result is a yes or no value representing color. If no, then red, if yes, then black. These results are called toggle. There are 27 of each toggle.

Origin

The value ranking for cards was initially developed as an initiative system. It still can be used as such, and it also works well for determining random timings (discussed in a later section). The names given to the corner results hint at the timing system that was originally developed. Eventually, the current initiative system evolved, and this usage was abandoned.

The unique number in the upper left provides a simple way to reference cards. Both the step and fragment are useful for random numbers within a given range that can also rarely produce extraordinary results outside the range.

Random Event Timing

During action time, it may be necessary to randomly determine when an event will occur. This can be done simply using the step and fragment. Draw a card and first check the step. If it is 1-4, that is the Phase during the turn the event will occur. If it is 0, it happens just before the round begins, if it is 5 it happens after the last other action resolves.

If more granularity is needed, the timing within the phase can be determined via the fragment. Treat the fragment as a Quickness value, rounding odd numbers down to even numbers. The numbers 1-3 happen after any 4 Quickness characters, and the 14 happens before any 12 with Quickness.

To preserve suspense, such as if the event is something momentous like when a bundle of dynamite explodes, the Judge should draw the card, check it, and place it face down. When it triggers, reveal it to the players and resolve the event.

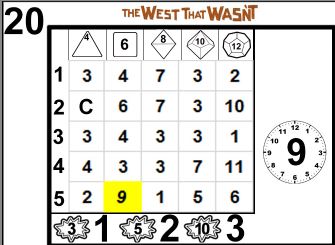
The Upper Results Section

An action card is divided into three sections, the outer edge, where the 4 corner results (discussed above) are located, the upper results section (the upper half of the box that separates the outer edge from the rest of the card) and the lower results section (the lower half of the box). An example of an upper results section is located below.

The Upper Grid

Most of the upper results section is a 5x5 grid (called the cause grid). This grid is used for all skill checks, to determine the pass/fail result. Because these results determine whether the action is successful, they are referred to as causes.

The grid is arranged with column headers shaped like polyhedral dice (along with a number representing the number of sides on the given die type), and row labels from 1-5. Each cell in the grid is one die of the given type. When speaking of a single given cell, the nomenclature is row-column, such as 3-8, for the d8 cell that has an 3 result (third row, above). When speaking of a result set, where multiple dice of a given type are rolled, the standard RPG convention of [row]d[column] is used, so for 3d8, the results of 7, 7 and 3 would be included (again, using the above image).

Cell Values

The values in each cell are results typical of that given die type. Therefore, the results in the d6 column tend to fall between 1 and 6 inclusive, just like a standard six sided die.

Hey, wait...how come there is a 9 in 5-6?

The die results are open ended, sometimes called "exploding". Many games use the concept of exploding dice, and there are multiple ways to implement them. The way the action card set implements open ended results combines simplicity and mathematical accuracy.

The concept of exploding dice is based on the idea that when the highest possible result on a given die type is generated, more dice can be thrown to increase the result. This makes it possible for dice of all sizes to be used, and for a d4 to achieve a success result even on a TN (target number) of 5 or more. On its face, it is a straight-forward idea.

However, when using dice for open ended results, the designer needs to choose between incomplete data sets and functional simplicity. Because the die is re-rolled when the highest possible result is generated, it becomes impossible to generate a value equal to any multiple of the value of the die face (6 for d6, for example) unless a check condition determines whether or not the die is re-rolled. This means that either the given result (the 6 in the previous example) is not a potential outcome (1, 2, 3, 4, 5, 7,... incomplete data set) or extra steps (a check condition) must be taken to allow this result to be obtained. Both choices are sub-optimal outcomes.

This does not mean it is impossible or unplayable. For example, in Warhammer Fantasy Roleplay 1st edition, damage was rolled on a d6. If a 6 was generated, the player rolled their attack again, and if it hits, the d6 may be rolled again and added to the previous result. If another six is rolled, it is rolled again and added recursively (no second instance of the check condition is necessary). This makes it possible to generate a 6 in damage (but not a 12 or 18, etc), at the cost of some convoluted rules and an extraneous die roll. This is an example of both a check condition and an incomplete data set. In this case, the data set is nearly always complete (assuming a 40% skill level the set is complete almost 99% of the time). Warhammer Fantasy Roleplay 2nd edition gave this operation a name, Ulrics Fury, and changed the die to a d10, making the data set complete even more often.

But still, more time is spent rolling, adding, and generally doing things that should not be necessary. Surely there is a better choice.

Another possibility is that when a die explodes, the new die is added, minus 1. This seems pretty simple at first. Now, any number can be generated and other than a simple subtraction, no more operations are necessary. Except that when that die explodes again, now 2 must be subtracted. This is just as bad as the previous possibility.

How do the action cards handle this? First of all, the card values are based on the average values generated on open ended dice, obtained by the following formula: n/2 + n/(n-1), where n is the number of sides on the given die. The results are distributed via a Monte Carlo approximation with the characteristic given average for each die type and 54 members in the set (one per each card). So that makes the card deck perform exactly like exploding dice, in a single step.

However, you may notice that some cells in the card section pictured above are bold, italicized and highlighted yellow. What is up with that?

With a set of 54, a good approximation of dice can be made, but the upper bound is not nearly as high as might be seen over years of play with dice. So each cell has 5 results (about 9%) that are marked as previously mentioned. These are called exceptional results. When an exceptional result is generated, another card is drawn and added. This continues recursively until a normal result is generated. All results are added.

This creates a substantially higher upper bound (see the examples in the exceptional results section of the action card tutorial, one of the results is a 22 on a d10), much closer to what gamers might see in the most extraordinary circumstances. It required the numerical characteristics to be adjusted a bit to preserve the average (so the cells still perform like the given die type), but it all happens seamlessly from the perspective of a player.

In some cases a result may be above the normal die maximum, but still not an exceptional result. This is because in 54 rolls, with only 9% being exceptional results, some "explosions" occur that are not in the top 9% of results. The set takes this into account and provides the necessary result.

Notes Regarding Exceptional Results

The reason exceptional results are bold, italicized and highlighted is to make them simple to identify, even if the user has vision impairment or difficulty with color. Since no other kinds of results need to be notated, it is feasible to use all three signifiers together for increased ease of use.

Exceptional results are optional. They can be used when the players deem necessary.

Critical Failures

The action cards also support a critical failure system, referred to as calamities. Calamities are denoted by a bold C in the given cell (as in 2-4 above). Each cell has one C in the deck. Rules for calamities are found in the using action resolution chapter.

Single Cell Versus Multiple Cells

You may be asking yourself why a multiple die result, such as 3d8, requires checking three separate cells rather than just displaying the result in a single cell. Should it not be possible to do the sampling automatically, so that the player need only to reference one cell and take the value displayed?

Yes!

In fact, the initial iterations of the action card deck did exactly this. The reason why that design was abandoned is that while elegant, it was thoroughly disliked by players. Understanding why requires some background regarding the math that powers the cards.

Each cell represents one entry in a 54 member set that approximates the given type of die. In the current iteration, all of the sets in a column are identical across the deck. In other words, if you took all 54 entries from 1-6 across the deck, and compared them to all 54 entries from 2-6, you would see the exact same distribution. This makes it simple to randomize the cells, because they are completely discrete. It doesnt matter at all if the 3-6 cell reads 4, and the 2-6 cell reads 6, as in the diagram above. The player can choose either.

However, if the player must use the designated cell only, then if a higher value exists in a cell represented by fewer dice, then players feel like they have been cheated, even though it is not true.

Why isnt it true? If the cells were sampled from the appropriate number of dice, unlike the current card iteration described in the previous example, if you took the 54 entries from 1-6 and compared them to the 54 entries of 2-6, the values are not equally distributed. The 2-6 results are higher on average (as they should be). But due to the nature of randomness, sometimes the result from more dice is lower (such as when one die rolls 6, while two dice roll 3 and 4), and though playtesters could understand this intellectually, it still led to a diminished gaming experience. This causes some design challenges.

In order to use the single cell model, one of the following choices must be made: either players must accept that sometimes a higher number will appear in a set of fewer dice, or the results must be engineered across the cards to ensure that this never occurs, rather than randomly distributing them. As a designer, I felt like the first choice was perfectly acceptable, but other players disagreed. The second choice is completely unacceptable. The purpose is to achieve randomness, engineering the results is the antithesis of that.

By using a single cell equals single die model, the issue is resolved in a simple way, but it does require a player choice instead of being completely automated.

Alright, I get it. Each cell is a single die. But if players are always choosing the die they want, the highest, then why can the results not be randomized, and then have the cells "corrected" to show the higher of either the number in the given cell, or any cell below? So, for example, in the image above, the 2-6 result remains 6, while the 3-6 and 4-6 results are updated to reflect 6 as well. Problem solved!

On the surface this seems like a workable solution. In effect you are randomizing the sample and then updating the value so that the player need not consult other cells. This presents numerous issues. The first of which is that by manipulating the values in the cells, the average is no longer preserved across the set, and the cards no longer perform like the dice they are meant to emulate. If the cards are only used one way, and there is only one possible card set, this might be acceptable, because, as illustrated, the given number will be chosen anyway.

But the cards are used in multiple ways. The simplest example is exceptional results. These are based on a single cell. When drawing a second card for an exceptional result, the value added is the one that corresponds exactly with the cell that produced the draw. Lower results are not allowed to be chosen (see the section on exceptional results in the using action cards chapter for a full explanation). Another example is multiple actions, where sometimes an action must use the 2nd (or lower) highest value in the set.

Another issue is that of perception. Take the example of the d6 column referenced in the conjecture. What was once a set of varied numbers becomes a block of 6s. This makes the card look superior to other cards. In one sense, it is (for skill checks). But the perception of randomness is distorted, and the entire reason all of this extra work was being done was to quell the perception of players.

The cards are displayed as they are to preserve the random characteristics they emulate. Additionally, they contribute to player confidence in them by virtue of the design choices that created them.

Exceptional Results

Unlike most resolution, with exceptional results only the specifically referenced cell in the cause grid is read. Why is this the case? Take a look at the cause grid of any card, for example this one:

For the following explanation, refer to the d12 column: 3, 11, 6, 12, 8. Assume these were dice being rolled at the table. If one die is rolled, the result is 3. If two dice are rolled, the results are 3 and 11. With three dice they are 3, 11, 6, etc. Only one of these results, the fourth one, could "explode". If these results were on dice at your table, you would pick up the die showing 12 on its face, and roll again (you might leave that die alone and pick up a different die to roll, but the effect is the same). The other 1-4 dice (depending on how many were initially rolled) would be completely ignored.

How do we simulate ignoring dice with action cards? Recall that action card concept 1 is use what you need and ignore the rest. You effectively treat the action card as if the other data are just blank space. When an exceptional result occurs another die of the appropriate type needs to be cast. This means drawing another card.

In the dice example, when you throw the new die, you do not throw the dice which occurred previously in the set, only the appropriate one. Only a single die is cast. When the result is generated, there is no choice to be made, because there is only a single die to be read. The question becomes, how do we define with cards which die that will be in a consistent way?

There are two possibilities that are simple and consistent. One is the way it is currently defined: always use the corresponding cell. This way there is no ambiguity, so it is the best choice. There is also a second choice that makes sense. Since the dice are arranged in an order within the set (the top result is checked first, and therefore is rolled first), theoretically, exceptional results could always be checked on the first row, and if a second (or subsequent) result is needed, further rows can be consulted.

This raises one issue regarding the upper bound. Unless the first row also has an exceptional result, checking the first row for other rows will lead to the possibility of 5 further draws, rather than 4, increasing the upper bound. This is an extremely unlikely occurrence, but it is possible. The effect on the math is small, but present. If you prefer this method, you may use it as long as everyone at your table agrees.

Hit Locations

Below the cause grid and burst results are four rectangles, each with a hit location written inside. Three of them have triangles to the left of them. The other one is the standard location. When performing an action that requires a hit location, these rectangles are used.

Why are there four locations, if only one is used?

The other three rectangles have two uses. One is with multiple hits due to automatic fire (such as from a Gatling gun). The next section discusses burst fire, consult the combat section of the rules for more information about determining hit locations for bursts. The other usage involves optional advanced rules.

If your group is utilizing the optional bump rules, the other three locations may be chosen. Bumps allow highly skilled characters to use their skill to change hit locations (among other things). See the section on bumps for more information.

Hit location results are generally arranged as they would be on the body, with the lower location more likely to hit a spot lower on the body. The bottom row has a few more leg hits, while the second one from the top an extra head hit. Otherwise, the bottom three results are identical. The top row, however, is significantly weighted towards vitals and head hits. This is because it requires two bumps to get to that box, and that takes a lot of skill (or luck), so it should be rewarded.

Burst Fire

Beneath the cause grid are three paired entries. The left number, 3, 5, or 10, located inside a burst icon, is the size of the burst. The right number is the number of successes. The three burst values use the same random seed. In other words, it is not possible to have a lower number of hits in the 5 (or 10) result than in the 3.

The difference between the size of the burst and the number of hits is called stray shots. In the case of a single shot, if it misses that is also considered a stray shot. Stray shots use the unintended targets section, on the right outer edge. See the combat section for rules regarding unintended targets.

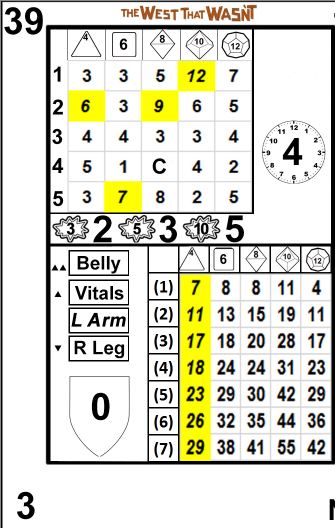
The Lower Results Section

The effect section is in the lower portion of the inner box of an action card. There are three possible results to be gleaned from the effect section: damage/victories, armor penetration, and hit location. An example effect section is located below.

The Lower Grid

The lower (effect) grid is on the right of the effect section. The grid is 5x7, and resembles the upper grid in that the columns are headed by polyhedral dice symbols and the appropriate number. The rows are numbered, similar to the upper grid, except these numbers are surrounded by parentheses. This allows the effect grid to be differentiated from the cause grid via discrete nomenclature. The third cell in the d8 column of the effect grid, which has a 20 (in the card section pictured above), is referred to as (3)8 (as opposed to 3-8 for the cause grid 3 result in the d8 column, or 3d8 for the 5, 9, and 3 results in the d8 column, both from the diagram in the cause section).

The effect grid is a sum of the given number and type of dice. Unlike the cause grid, the results in the effect grid are arranged such that a greater number of the same die type always leads to a greater result on the same card. This is much simpler to engineer than in the cause grid, because the results are summed rather than sampled. Also, it allows for game effects to increase the size of an effect pool without the possibility of reducing the effect magnitude.

Generating Victories and Wounds

The effect grid is used to generate victories (also damage). The standard magnitude necessary for a wound or victory is 6.

If victories and damage both increment on 6, why not just list total victories/wounds instead of requiring division?

There are multiple reasons behind this decision. The first is that when damage is dealt, any leftover magnitude is applied as concussion (see the combat section). There are also some weapon types that deal damage entirely in concussion.

Finally, however, by having the full result the size/victory threshold can be modified as necessary. For example, an extremely large adversary may have a size (the number required to achieve a wound, see the combat section) greater than 6. One character may have an advantage over another in a contest, which allows them to have a lower victory threshold. The possibilities are endless, and this design choice allows the flexibility for the Judge to vary challenge as the story dictates.

Exceptional Results

Like the cause grid, exceptional results can be generated in the effect grid. Unlike the cause grid, however, exceptional results are not differentiated by cell. Because the members of each column (in other words, an entire die type) are grouped into a single set (which ensures the increasing magnitude as the number of dice increase), exceptional results apply to entire columns. The column is shaded yellow, and the font is bold and italicized. The d4 column in the referenced card has exceptional results.

Armor Penetration

In the lower left of the lower portion of the inner rectangle of the action card is a shield with a numeral inside. This represents armor penetration. See the combat section of the rules for an explanation of how to use these results.

The range of values is +2 to -2. The results are arranged in a bell curve, with the majority of values being 0. Negative values are in red font, positive values (and zero) are in black.

Equipment Failure

In the upper right of the card above the clock face is the equipment failure section. If a broken wrench appears, then a red number will also be present. This number is compared to the reliability of the equipment being used (if any) to determine if breakage occurs. See the gear section for more information.

There are a total of 13 equipment failure results (besides no result). This means the least reliable type of gear can fail approximately 24% of the time. Only improvised and previously damaged gear falls into this category. The highest reliability gear fails significantly less than 1% of the time.

Equipment failure rules are optional. If nothing appears above the clock face, equipment failure is not possible.

Scatter

The final result in the cause section is a clock face and number. The value is 1-12, with 4 of each odd result and 5 of each even result. The clock face is used to determine random cardinal directions (though a random time of day is also possible when used in conjunction with the number). See the combat section of the rules for how to use the scatter diagram.

Unintended Targets

On the right outer edge of the cards are figures representing potential unintended targets. Any ranged attack that generates stray shots can potentially hit unintended targets. Each card has up to four figures with a number from 1 to 10. See the unintended targets section of the combat chapter for rules on how to interpret the results.

The current iteration of the unintended targets favors simplicity over variability and "accuracy". The procedure involves checking the numbers on the figures, and, if the number is equal to or less than the number of stray shots then the closest (or most likely, as determined by the Judge) unintended target is hit. This is simple, and also gives the narrative control to the Judge for maximum dramatic effect. If multiple figures have numbers less than potential targets, then multiple targets can be hit.

Note: This is not how the initial idea was implemented. In the prior rules set, each potential unintended target is given a number, and if any stray shots exist, the figures are checked. If a figure has an x over it, then the unintended target with that number (counting from the top of the card) is hit. In this manner, even the least likely target can be hit when only one stray shot is present. This increased variability does come at a cost, because the Judge will need to arrange the potential targets somehow such that after the card is drawn it can be determined which one, if any, is actually hit.

Also note that unintended targets can be used in situations such as a stagecoach driving into a crowd or a bunch of TNT detonating in a mine shaft, so it might not always be related to weapon results.

Why Action Cards?

Most tabletop RPGs use dice. Often the mechanics around the dice may be novel, but in general, dice are well understood by the gaming public. Many other games use cards for their resolution mechanics, but few if any use cards as packed with data as those provided with this game. From the perspective of a new gamer, considering TWTW for their table, why would I want to learn to use these action cards? What value do they bring to the table that is not provided by more familiar mechanics and tools?

How about this, first. Why did I decide on action cards? Speed. Er, I mean detail. Actually, speed. Wait, speed and detail. The cards were created to find the optimum intersection of speed and detail. Final answer.

Many game systems have a to hit roll. Many also include hit location. Many include armor penetration or protection in some way. Many include an initiative system, and some of those modify initiative by the action chosen and/or character attributes. A few include stray shots and equipment failure. Many systems, however, ignore most, if not all, of these subsystems.

Why is that? Over the years I have played a lot of systems. My preference has generally been for games with more detail and more mechanical depth (big surprise, right?). Part of the reason for that is that I have a huge advantage in that it is very easy for me to memorize large sets of data. I have memorized the hit location charts for many games, and even can recite the damage adjustments each location offers. Many players cannot (or will not) do this. Many of those players find the time spent rolling extra dice and referencing charts and tables to be wasted time; the value gained by this extra information is not commensurate with the time spent generating it. At my table, I find myself calculating all of this stuff for all the other players, because it is faster that way and they prefer that over looking it up.

Besides players at my table, I have talked to many others, both in person and online, about gaming and their system preferences. Of the players who do not like systems that include the extra detail mentioned above, many different reasons were given. The most common reasons to dislike the system are remembering to actually use the added steps, remembering how to use the steps/which tables to reference, the time spent to use the steps and/or too many mistakes when trying rarely used rules. Very few people said they did not want the detail and information the rules provided, instead they did not like the format and/or delivery system. They felt that the "over-complication" could break immersion or otherwise be jarring. In most cases the rules themselves are not actually complicated at all, but adding additional steps feels complicated, even when it is just a simple roll.

What breaks immersion? Arguing about rules. Looking things up in books and tables. Rolling unnecessary dice, or spending more than a few seconds fiddling with rules that do not make the game, and story, move forward.

Back to the action cards. How do they prevent the immersion breaking faux pas?

1. The action cards "know" the rules. Once you understand how to use the cards, you almost never have to refer to a rulebook for anything. All that is needed are the cards and your character sheet. Almost no extra effort is required.
2. Because of how the cards are organized, the order of operations is always clear, and rules, even rarely used ones, are never forgotten. You know that guy who always seems to forget to check if his weapon breaks? Action cards have you covered.
3. All of the results that are necessary for any action, no matter the complexity, are complete in a single card flip.

The goal of action cards, as initially envisioned, was: resolve anything in 30 seconds or less, and sacrifice no detail. The first part doesnt sound like such a big deal, most things are easily done in that time. In fact, most resolutions in most games are 5 seconds or less.

Same with cards! The value gained via action cards increases as the complexity of the action increases. Performing a simple skill check with dice or cards takes 3 seconds or so. However, performing an attack action involving to hit, location, armor penetration, potential equipment failure, damage, unintended targets...this can be a long series of rolls and multiple book/table/chart references. With action cards its still a single flip, and even with all that detail it is done in 30 seconds or less every time, with no reference errors.

The action cards do not make the game the fastest on the market. Instead, they allow a mechanically deep game to be delivered at a speed comparable to other games, but with significantly increased detail and reduced extraneous activity. I contend they also reduce errors, but I do not have data to prove this.

The vision of action cards came in an instant, but the actual implementation and design of the card mechanics was a long process. However, that work only needed to be done once. There is a learning curve to the action cards, but it is not as steep as it seems at first glance.

Spend a few minutes reading the action card introduction chapter, and try some sample actions. The time you invest in learning to use this tool will be paid back with increased fluidity, detail and immersion at the table.

Extensibility

Another advantage the action card set offers is the ability to use the same math to add new result sets very quickly and easily. A d14 may exist, but I have never seen one and they are certainly not common. However, the math for such a result set is simple to produce. If it became valuable to have further die types, such as for highly skilled and experienced characters, the cards could easily be extended to accommodate this.

Additionally, the given results sets are distributed in a uniform and smooth manner. If a game required a wider possibility range, one that had more high and low results and fewer mid-range results (to facilitate a pulp style game, for example), this could also easily be created.

Even without varying the range the results as given could be redistributed many ways to lead to multiple unique card sets. The possibilities are nearly endless.

Believe it or not, there are more potential shuffles of a 54 card deck than stars in the known universe, or atoms in the earth itself.